Frames

Basic use

The problem to be solved

We want to compute the Doppler effect of a satellite with respect to a ground station.

A simple solution

On the one hand, we define the Local Orbital Frame (LOF) related to the satellite.

Let’s first define some initial state for the satellite with:

  • an inertial frame
  • a date in some time scale
  • a central attraction coefficient
  • an orbit defined by the position and the velocity of the satellite in the inertial frame at the date.

The initial orbit is just set as a CartesianOrbit. More details on the orbit representation can be found in the orbits section of the library architecture documentation.

Frame inertialFrame = FramesFactory.getEME2000();
TimeScale utc = TimeScalesFactory.getUTC();
AbsoluteDate initialDate =
    new AbsoluteDate(2004, 01, 01, 23, 30, 00.000, utc);
double mu =  3.986004415e+14;
Vector3D position = new Vector3D(-6142438.668, 3492467.560, -25767.25680);
Vector3D velocity = new Vector3D(505.8479685, 942.7809215, 7435.922231);
PVCoordinates pvCoordinates = new PVCoordinates(position, velocity);
Orbit initialOrbit =
    new CartesianOrbit(pvCoordinates, inertialFrame, initialDate, mu);

As a propagator, we consider a simple KeplerianPropagator.

Propagator kepler = new KeplerianPropagator(initialOrbit);

So, the LOF is all defined, assuming its type to be QSW.

LocalOrbitalFrame lof =
    new LocalOrbitalFrame(inertialFrame, LOFType.QSW, kepler, "QSW");

On the other hand, let’s define the ground station by its coordinates as a GeodeticPoint in its own TopocentricFrame related to a BodyShape in some terrestrial frame.

double longitude = FastMath.toRadians(45.);
double latitude  = FastMath.toRadians(25.);
double altitude  = 0.;
GeodeticPoint station = new GeodeticPoint(latitude, longitude, altitude);
Frame earthFrame = FramesFactory.getITRF(IERSConventions.IERS_2010, true);
BodyShape earth = new OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
                                       Constants.WGS84_EARTH_FLATTENING,
                                       earthFrame);
TopocentricFrame staF = new TopocentricFrame(earth, station, "station");

More details on BodyShape and GeodeticPoint can be found in the bodies section of the library architecture documentation. More details on TopocentricFrame can be found in the frames section of the library architecture documentation.

Finally, we can get the Doppler measurement in a simple propagation loop

AbsoluteDate extrapDate = initialDate;
while (extrapDate.compareTo(finalDate) <= 0)  {

    // We can simply get the position and velocity of station in LOF frame at any time
    PVCoordinates pv = staF.getTransformTo(lof, extrapDate).transformPVCoordinates(PVCoordinates.ZERO);

    // And then calculate the doppler signal
    double doppler = Vector3D.dotProduct(pv.getPosition(), pv.getVelocity()) / pv.getPosition().getNorm();

    System.out.format(Locale.US, "%s   %9.3f%n", extrapDate, doppler);

    extrapDate = new AbsoluteDate(extrapDate, 600, utc);

}

Here are the results displayed by this program:

          time           doppler (m/s)
2008-10-01T00:00:00.000   -2925.114
2008-10-01T00:10:00.000   -3069.084
2008-10-01T00:20:00.000   -1331.910
2008-10-01T00:30:00.000    1664.611
2008-10-01T00:40:00.000    3143.549
2008-10-01T00:50:00.000    2832.906
2008-10-01T01:00:00.000    1556.662
2008-10-01T01:10:00.000    -140.889
2008-10-01T01:20:00.000   -1860.637
2008-10-01T01:30:00.000   -3195.728
2008-10-01T01:40:00.000   -3538.053

Source code

The complete code for this example can be found in the source tree of the library, in file src/tutorials/fr/cs/examples/frames/Frames1.java.

Advanced use

The problem to be solved

The problem is related to the one exposed in the User defined frames subsection of the frames section of the library architecture documentation.

It can be summarized by the following schema.

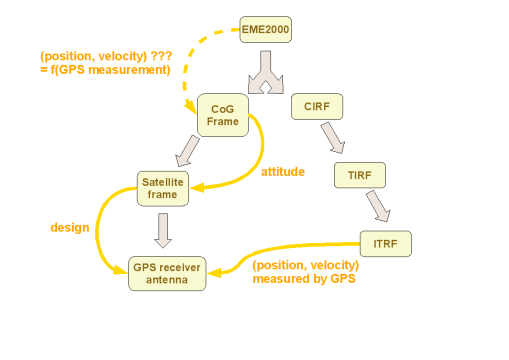
frames 2 tutorial

For a given satellite, GPS measurements for position and velocity, expressed in the ITRF frame, are available at any moment. The GPS antenna is fixed with some offset with respect to the satellite reference frame. The attitude of the satellite reference frame with respect to some moving frame related to the satellite center of gravity (CoG) is known at any moment. We want to compute for some instant the position and velocity of the CoG in the EME2000 inertial frame.

A smart solution

A possible solution provided by OREKIT is detailed above.

The CoG frame has its origin at the satellite center of gravity and is aligned with EME2000. It is linked to its parent EME2000 frame by an a priori unknown transform which depends on the current position and velocity. This transform is what we want to compute.

We first build the frame. We use the identity transform as a simple dummy value, the real value which is time-dependent will be recomputed when time is reset:

Frame cogFrame = new UpdatableFrame(FramesFactory.getEME2000(), Transform.IDENTITY, "LOF", false);

The satellite frame, with origin also at the CoG, depends on attitude. For the sake of this tutorial, we consider a simple inertial attitude here:

Transform cogToSat = new Transform(new Rotation(0.6, 0.48, 0, 0.64, false));
Frame satFrame = new Frame(cogFrame, cogToSat, "sat", false);

Finally, the GPS antenna frame is always defined from the satellite frame by 2 transforms: a translation and a rotation. Let’s set some values:

Transform translateGPS = new Transform(new Vector3D(0, 0, 1));
Transform rotateGPS    = new Transform(new Rotation(new Vector3D(0, 1, 3),
                                                    FastMath.toRadians(10)));
Frame gpsFrame         = new Frame(satFrame,
                                   new Transform(translateGPS, rotateGPS),
                                   "GPS", false);

Let’s consider some measurement date in UTC time scale:

TimeScale utc = TimeScalesFactory.getUTC();
AbsoluteDate date = new AbsoluteDate(2008, 10, 01, 12, 00, 00.000, utc);

Then let’s get some satellite position and velocity in ITRF as measured by GPS antenna at this moment:

Vector3D position = new Vector3D(-6142438.668, 3492467.560, -25767.25680);
Vector3D velocity = new Vector3D(505.8479685, 942.7809215, 7435.922231);

The transform from GPS frame to ITRF frame at this moment is defined by a translation and a rotation. The translation is directly provided by the GPS measurement above. The rotation is extracted from the existing tree, where we know all rotations are already up to date, even if one translation is still unknown. We combine the extracted rotation and the measured translation by applying the rotation first because the position/velocity vector are given in ITRF frame not in GPS antenna frame:

Transform measuredTranslation = new Transform(position, velocity);
Transform formerTransform =
    gpsFrame.getTransformTo(FramesFactory.getITRF(IERSConventions.IERS_2010, true), date);
Transform preservedRotation =
    new Transform(formerTransform.getRotation(),
                  formerTransform.getRotationRate());
Transform gpsToItrf =
    new Transform(preservedRotation, measuredTranslation);

So we can now update the transform from EME2000 to CoG frame.

The updateTransform method automatically locates the frames in the global tree, combines all transforms and updates the single transform between CoG itself and its parent EME2000 frame.

cogFrame.updateTransform(gpsFrame, FramesFactory.getITRF(IERSConventions.IERS_2010, true), gpsToItrf, date);

The frame tree is now in sync. We can compute all position and velocity pairs we want:

PVCoordinates origin  = PVCoordinates.ZERO;
Transform cogToItrf   = cogFrame.getTransformTo(getITRF(IERSConventions.IERS_2010, true), date);
PVCoordinates satItrf = cogToItrf.transformPVCoordinates(origin);

Transform cogToEme2000   = cogFrame.getTransformTo(FramesFactory.getEME2000(), date);
PVCoordinates satEME2000 = cogToEme2000.transformPVCoordinates(origin);

As a result, we can compare the GPS measurements to the computed values:

GPS antenna position in ITRF:    -6142438.668  3492467.560   -25767.257
GPS antenna velocity in ITRF:     505.8479685  942.7809215 7435.9222310
Satellite   position in ITRF:    -6142439.167  3492468.238   -25766.717
Satellite   velocity in ITRF:     505.8480179  942.7809579 7435.9222310
Satellite   position in EME2000:  6675017.356 -2317478.626   -31517.554
Satellite   velocity in EME2000: -150.5212980 -532.0401625 7436.0739039

Source code

The complete code for this example can be found in the source tree of the library, in file src/tutorials/fr/cs/examples/frames/Frames2.java.

Direct use of transforms : coordinates with respect to spacecraft frame

The problem to be solved

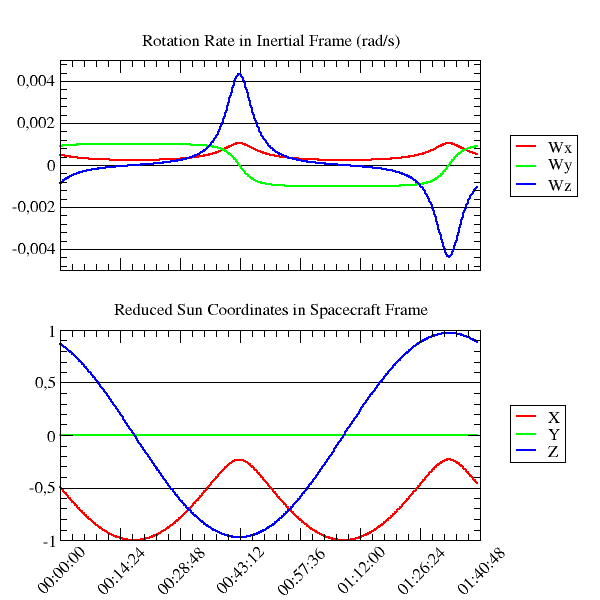
Let’s consider a spacecraft which attitude is guided by a yaw steering law, we want to plot some of the effects of such a law on the spacecraft motion.

An immediate solution

There was once a SpacecraftFrame in Orekit, but it could not be used in master propagation mode and has been deprecated as of 6.0, so we won’t use it. First, an initial orbit for the spacecraft is defined as follows:

Frame eme2000 = FramesFactory.getEME2000();
AbsoluteDate initialDate = new AbsoluteDate(1970, 04, 07, 0, 0, 00.000,
                                            TimeScalesFactory.getUTC());
double mu =  3.986004415e+14;
Orbit orbit = new CircularOrbit(7178000.0, 0.5e-4, -0.5e-4,
                                FastMath.toRadians(50.),
                                FastMath.toRadians(220.),
                                FastMath.toRadians(5.300),
                                PositionAngle.MEAN,
                                eme2000, initialDate, mu);

More details on the orbit representation can be found in the orbits section of the library architecture documentation.

Then the attitude law for the spacecraft is constructed:

  • we first define a nadir pointing law towards the Earth under the spacecraft,
  • then a yaw steering law is added

The yaw steering law wraos the nadir point law in order to give maximal lightning to the solar arrays, which rotation axis is Y in spacecraft frame:

Frame earthFrame = FramesFactory.getITRF(IERSConventions.IERS_2010, true);
BodyShape earth = new OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
                                       Constants.WGS84_EARTH_FLATTENING,
                                       earthFrame);
NadirPointing nadirLaw = new NadirPointing(earth);

final PVCoordinatesProvider sun = CelestialBodyFactory.getSun();
YawSteering yawSteeringLaw = new YawSteering(nadirLaw, sun, Vector3D.MINUS_I);

More details on the attitude representation can be found in the attitudes section of the library architecture documentation.

As a propagator, we consider an analytic EcksteinHechlerPropagator.

Propagator propagator =
    new EcksteinHechlerPropagator(orbit, yawSteeringLaw,
                                  Constants.EIGEN5C_EARTH_EQUATORIAL_RADIUS,
                                  Constants.EIGEN5C_EARTH_MU,
                                  Constants.EIGEN5C_EARTH_C20,
                                  Constants.EIGEN5C_EARTH_C30,
                                  Constants.EIGEN5C_EARTH_C40,
                                  Constants.EIGEN5C_EARTH_C50,
                                  Constants.EIGEN5C_EARTH_C60);

More details on Propagator can be found in the propagation section of the library architecture documentation.

Then, we associate a step handler with the propagator which directly computes the desired data in spacecraft frame using the current spacecraft state

propagator.setMasterMode(10, new OrekitFixedStepHandler() {

    public void init(SpacecraftState s0, AbsoluteDate t)
        // write file header
    }

    public void handleStep(SpacecraftState currentState, boolean isLast)
        throws PropagationException {

        Transform inertToSpacecraft = currentState.toTransform();
        Vector3D sunInert = sun.getPVCoordinates(currentState.getDate(), currentState.getFrame()).getPosition();
        Vector3D sunSat = inertToSpacecraft.transformPosition(sunInert);
        Vector3D spin = inertToSpacecraft.getRotationRate();

        // write data to file

    }

}

So, computing over an orbit, we can plot the following results showing clearly a typical yaw steering behavior:

Frames 3 tutorial

Source code

The complete code for this example can be found in the source tree of the library, in file src/tutorials/fr/cs/examples/frames/Frames3.java.